ナマステ!
インドで買い物をすると、5%、12%、18%、28%の4種類の税率(ほかにも0%、0.25%、3%)があったり為替相場が1ルピー=1.6円程度だったり、すこしいいレストランだとサービス料が10%追加でかかったりして、暗算で金額を計算しようとすると難しいかもしれません。
暗算でパッと金額を計算できると、「この人頭いい⁉」と思われるかもしれないのでできるようにトレーニングしてみてはいかがでしょうか。
それでは記事に移ります。
Contents
11 x 2桁の計算はかなり計算が楽で覚えておくと便利
例えば為替相場でドル円相場では1ドル=110円程度であります。(2019年6月1日現在は1ドル=108.362円)
なのでドルで買い物をするときのざっとした計算で使えると思います。
また次の計算ですが、紹介する計算方法で瞬殺できます。
例えば11x23= 253、11x34= 374、11x56 = 616
①まず 11x 23 は 2〇3 と百と一の位はすぐに計算できます。
②次に〇の部分は2+3=5 で十の位が決まります。
これで答えが253となります。
同様に、次に11x34= 374 ですが、
①11 x 34 = 3〇4 、②〇=3+4=7 となり、374と答えが出ます。
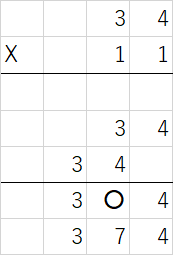
たまに11x56 = 616 のような百の位が増えることもあるのでご注意ください。
ちなみに11x 3桁の場合は千と一のくらいは同様にすぐにきまりますが、百と十の位はさらに計算する必要があります。2桁の掛け算のときの十の位の数字の出し方と同じ要領です。
②百の位の数と十の位の数=〇、③十の位と一の位=△の計算
たとえば324 x 11 = 3564ですが、
①11X324 = 3〇△4、
②〇=3(百の位)+2(十の位)=5
③△=2(十の位)+4(一の位)=6
①~③より3564となります。
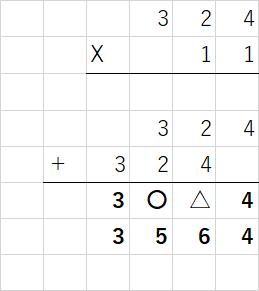
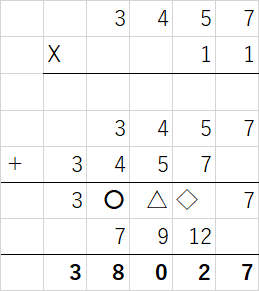
5、25、50の掛け算は 割り算を使うと簡単に求まる
5の計算
インドで外食に行くとたいてい5%のGST税がかかります。(ホテル併設のお店は12%)
この場合の5%の税金額は
まず①10%の金額を出します。(×0.1するだけ)
次に②この10%から2で割ることで算出できます。
例えば480Rsとすると
①480 x 0.1= 48。
②48 ÷ 2 = 24でGST税は24Rsとなりました。
あとは暗算で480 + 24 = 504 となります。
頭の中で最初の480Rsを覚えておく必要があるので少し難易度があがります。
また25の倍数の場合は
25 = 100 ÷ 4
であることを意識しましょう。
例えば380 x 25の計算するときは、
380 x 25
= 380 x (100 ÷ 4)
= (380 ÷ 4 (= 95)) x100 (計算順序を入れ替えた。4の割算の暗算方法は下記で解説)
= 9500
50 の計算の場合は 100 ÷ 2 か 上の5の掛け算で出した要領に10倍するとよいでしょう。
4の割り算は重要
4は2 x 2なので4の割り算をするときは2回2で割ると考えてもいいかもしれません。
78 ÷ 4 = 39 ÷ 2 = 19.5
84 ÷ 4 = 42 ÷ 2 = 21
3800 ÷ 4 = 1900 ÷ 2 = 950
上のように25の倍数を計算する際に25 = 100 ÷ 4を算出するのに役だったりするので重要です。
25 = 5 x 5 でも出せますが100をかけて4で割ったほうが楽な気がします。
掛け算の時も同じ要領でx2x2と2回2でかけてみるとスムーズに計算できたりします。
因数分解の考えを活用する
39 x 16 =
の計算であれば、
28 x 29 =
28 x (30 - 1) =
840- 28 = 812 となります。
25 X 33
GST税の計算に戻りますが、
12%であれば、12= 4 x 3で因数分解して計算してみたり
75Rs x 4 x 3 (%)= 300Rs x 3(%)= 9Rs
18%でも同様に2 x 9や3 x 6に分解して計算しなおしてみたり
80Rs x 3 x 6 = 240 x 6 (%) = 1440(%) = 14.4Rs
28%でも4 x 7などに分解して計算しやすくすると、ざっと答えを出せるのではないでしょうか?
1ルピー(Rs)=1.6円を日本円に換算するときの計算でも
1.6 = 4 x 0.4 と因数分解して計算しやすくすることもできます。
正確な計算は電卓に任せるのがよいとは思いますが、ざっと計算するには因数分解して計算しやすくし直すのが便利ではないかと思います。
2桁の二乗の計算は公式を活用する
(a + b)^2 = a^2 + 2ab + b^2
a^2-b^2 = (a+b)(a-b)
たとえば次の計算のように活用します。
16^2 = (20-4)^2 = 400 - 160 + 16 = 256
78 x 82 = (80-2)(80+2) = 6400 - 4 = 6396
2のべき乗を覚えよう
2^2=2x2=4
2^3=2x2x2=8
2^4=2x2x2x2=16(4^2、4の2乗)
2^5=2x2x2x2x2=32
2^6=2x2x2x2x2x2=64(4^3、4の3乗)
2^7=2x2x2x2x2x2x2=128
2^8=2x2x2x2x2x2x2x2=256(4^4、4の4乗)
2^9=2x2x2x2x2x2x2x2x2=512
2^10=2x2x2x2x2x2x2x2x2x2=1024
です。2の10乗が1024であることは有名かもしれませんが、
2の7乗=128であることを覚えておけば便利かもしれません。
2の6乗=64であればすぐに計算できるので2の7乗も覚えておけば良いかもしれません
2^3=8を利用して2^6=2^3x2^3=8x8=64を出せるからです。
また16の2乗であれば、2^4x2^4で2の8乗なので2^7x2=128x2で1発で256と出せます。
2桁同士の掛け算で〇5 x 〇5 となるパターンを覚えよう
〇5 x 〇5という珍しいパターンですが、この暗算も瞬殺できます。
答えは、上2桁が〇x(〇+1)+下2桁が25となります。
たとえば85 x 85であれば
85 x 85 = 7225となります。
上2桁が8x(8+1)=72で、
下2桁が25
となり、7225となります。
他には下記のとおりです。
25x 25 = 625
35x 35 = 1,225
45x 45 = 2,025
55x 55 = 3,025
65x 65 = 4,225
75x 75 = 5,625
85x 85 = 7,225
95x 95 = 9,025
の9パターンとなります。
ざっと計算するときの近似値を出すときとかに利用するのが良いと思います。
2桁 x 1桁 の掛け算に慣れよう!
日本人であれば九九は覚えているでしょう。
九九を覚えているため、一瞬で1桁同士の掛け算の答えを導きだせます。
今度は少しレベルアップさせて2桁x1桁を数秒で暗算できるようにトレーニングをすることで
2桁 x 2桁 の掛け算であっても片方の数字を丸めて(近似させて)計算することで、それなりに近い答えを導きだすことができます。
たとえば28 x 34 の計算であれば
30 x 34と近似的に考えて、だいたい1020より60ぐらい(正確には68)少なく960くらいかと目安を出すことができます。(正確には952)
次に2桁 x 1桁の暗算ですが、
①1桁同士の掛け算を2回行う必要があり、その結果をどちらとも覚えておく必要があること
②①の結果を足し合わせる必要があること
の2つの過程があるので少しレベルがあがります。
慣れればそこまで難しくはないと思いますので、ちょっとしたトレーニングをしてみましょう。

ちなみに2桁同士の掛け算の場合は
①1桁同士の掛け算を4回行う必要があり、すべて覚えておく必要があること
②①の結果を足し合わせる必要があること
4つも計算結果を覚えておき、すべて足し合わせる必要があり、覚えてられません(笑)

たとえば48 x 34の計算であれば 50 x 34 = 1700 - 2 x 34 = 1632 のように
近似的に2桁 x 1桁でひとまず計算して、その後足し算引き算で調整するのが簡単でしょう。(それでも計算間違いが起こりえますが)
10の何乗かを覚えよう
1,000,000,000,000はいくらでしょうか?
答えは後でわかります。
欧米圏の数字編
1,000,000が1millionで100万(10の6乗)
1,000,000,000が 1billion で10億(10の9乗)
1,000,000,000,000 が1trillionで1兆(10の12乗)
問題の答えは1兆でした。
インド特有の区切り方
1crore = 10,000,000(10の7乗です。)
インドのニュースでたまに出てくる1 lakh crore という数字はいくらかというと
1lakh(10の5乗) x 1crore(10の7乗) =1兆(10の12乗) となります。
日本特有の区切り方
日本の単位ですが、
・億の単位は100,000,000で10の8乗です(10の8乗)
・兆の単位は100,000,000,000で10の12乗です(10の12乗)
1万といえば100x100ですね。
この100x100は10の2乗同士の掛け算だから、1万は10の4乗という確認ができますね。
また1万(10の4乗) x 1万 = 1億(10の8乗)となります。
さらに1万 x 1億 = 1兆となります。(日本は4桁区切りであるから当たり前かも知れません)
ちなみに100万×100万も1兆となります。
100万は10の6乗で、1兆は10の12乗だからです。
では最後に問題です。
1兆 ÷ 10万 =?
答えは1千万でした。(10の12乗÷10の5乗=10の7乗となり10,000,000)
以上ご確認してみてください。
まとめ
インド式計算方法が一時はやりました。
私はブームに乗らず結局知りませんが、海外にいると支払い時に通貨レートの影響だったりで暗算力が鍛えられると思います。
インドは数に強いといわれているので負けないように頑張りたいと思います。
数年前に読んだ本で
参考になる本があるので紹介したく思います。
『完全版 暗算の達人 世界最高の高速暗算テクニック』アーサー・ベンジャミン 、 マイケル・シェルマー
レベルが高すぎて正直ついていけませんでしたが、簡単な順番で暗算していくなど、ためになる項目が多かったです。簡単な暗算から高難易度の暗算3桁x3桁等の計算方法があります。
また読み返して暗算スキルを身に着けていきたいと思います。よかったら読んでみてください。
国によって数の数え方や桁の概念が変わりごちゃごちゃしますが、10のなん乗であるかを覚えておけばスムーズに計算ができるのが面白いと思えるかもしれませんね。
あと、上記に記載しませんでしたが、19x19までのかけ算の表を添付しています。
インド人も人によってまちまちですが19x19までは覚えている人はほとんどいないようです。
結局、結論としては
計算が速い人は大量にいろいろと計算をこなしてきて、計算結果を覚えているから早いのではないか
と思います。
余裕があれば覚えるようにするのもいいかもしれません。
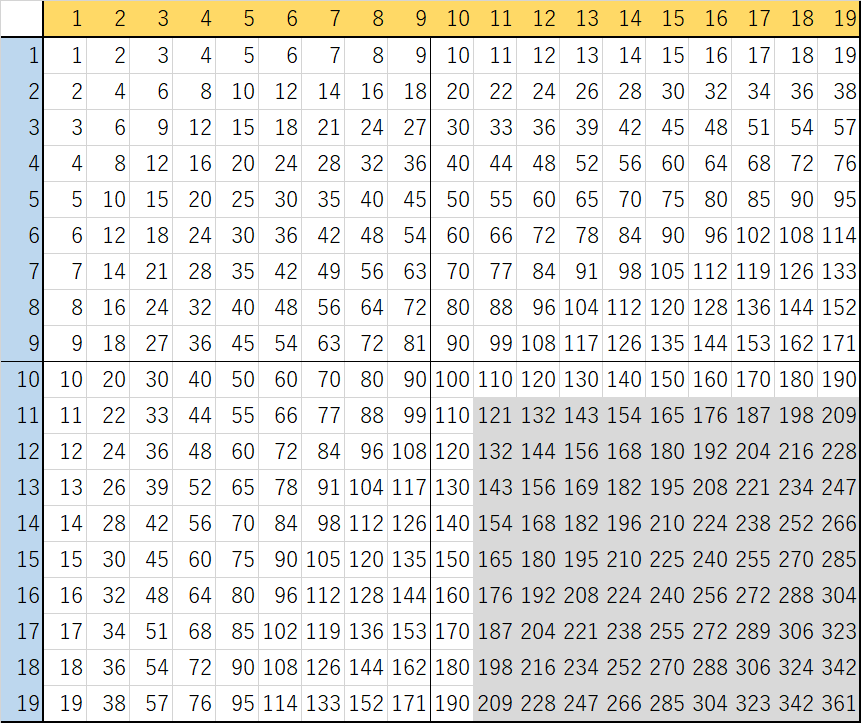
11~19の2桁同士の掛け算部分のみ色を付けてあります。
パッと計算できれば、コイツできるっっ、と思われるのでマスターしてくださいね。
以上読んでいただきありがとうございました。ダンニャワード!